I have always found astronomy and cosmology fascinating since I was a boy, and so I follow several science blogs. Recently two of them published interesting blog posts on probability and Bayes Theorem. Even if you’re not much interested in maths, I think there’s plenty worth looking at in these posts.
Bayes Theorem for non-mathematicians
Bayes Theorem is a formula for calculating a new probability of a hypothesis being true, after new evidence is considered. It is based on the idea that if a new piece of evidence is more likely if a hypothesis is true than if it is false, then it raises the probability that the hypothesis is true.
One new piece of “positive” evidence doesn’t necessarily make the event highly probable, just more probable than it was before, to a degree that can be mathematically demonstrated.
For example, a heavy smoker has developed a bad cough and fears he may have lung cancer, though he has no other symptoms. He insists on having tests. His doctor knows, based on population statistics, that about 15% of active male smokers develop lung cancer at this man’s age. The doctor orders a CT scan, which returns a positive result, but the doctor also knows that CT Scans have a false positive probability of about 20%. So what is now the probability that the smoker has lung cancer? Bayes Theorem allows the new probability to be calculated (and if my maths is correct, the new probability is about 40%).
Probability and the resurrection of Jesus
Aron Wall is a postdoctoral researcher studying quantum gravity and black hole thermodynamics, and blogs at Undivided Looking. He is a christian, and his blog covers many aspects of physics, mathematics, philosophy and christian belief.
A recent post, Black Swans examines the probability that Jesus really was resurrected, based on a reader asking about an argument that goes like this:
- For every dead person, 99.9999…% of the time God does not intervene.
- Jesus died.
- Therefore, we can be 99.9999….% certain that God did not intervene in Jesus’ death.
Therefore, the reader asks, isn’t it true that no matter how much evidence there is for the resurrection, the prior probability in a Bayes analysis will always be so low that the final probability (known as the posterior probability) must always be very low?
Aron’s response
I learnt a lot from Aron’s response, which started by presenting the following parallel argument:
- For every American citizen who lives during a presidential election, 99.9999…% of the time they do not become President.
- Barack Obama was a living American citizen in 2008.
- Therefore, we can be 99.9999….% certain that Barack Obama did not become President of the United States.
Obviously this argument is false, but why? Aron points out that the argument might be true for a randomly selected American, but Obama belonged to a small class of people who are much more likely to become President – a candidate with certain gifts and aspirations. With that additional information, premise 1 is not applicable to him.
So, he suggests, Jesus too belongs to a small class of people – someone who claimed to be the Messiah, did miracles, even predicted his resurrection – and so the probabilities of randomly selected people being resurrected don’t apply to him.
There’s a lot more in the post about probability assumptions and calculation, but one other example seemed especially helpful. He discusses how Europeans used to think all swans are white, because they were the only swans they saw in Europe. Drawing the conclusion that all swans are indeed white might be valid if the swans they observed in Europe were randomly selected from the world population of swans. But they are not. All swans in Europe were white, but there are many black swans in Australia. The inference was based on a non random selection.
The lesson is that we have to be careful when estimating probability not to assume observations or conclusions are random when in fact they are not, but of a special class. We may disagree about the evidence for the resurrection, but it is important to try to frame the argument properly.
Understanding probability
I have referenced Luke Barnes and his blog, Letters to Nature several times before. Luke is a Postdoctoral Researcher in cosmology and astrophysics, and has taken a particular interest in the scientific evidence that the universe is surprisingly “finely-tuned” for life.
Luke has had a running “battle” with historian Richard Carrier about the science and probability of fine-tuning. Luke is (apparently) an agnostic or perhaps, more recently, a deist or theist (he doesn’t discuss his beliefs much), while Richard is an atheist.
A while back I reported how their argument about fine-tuning was judged by Carrier’s friend and fellow atheist JJ Lowder as being decisively won by Barnes – not surprising since Barnes was arguing on his area of expertise and Carrier was not.
The argument resumes
Recently Richard Carrier resumed the argument about fine-tuning, sometimes using probability, and Barnes responded with two posts mainly on the fine-tuning and two (here and here) on probability – which is what I’m focusing on here.
Three main issues are involved:
- The science of fine-tuning
- The theistic argument based on fine-tuning
- Understanding probability
The science of fine-tuning
As you’d expect, Carrier fares worst again on the science, because Barnes knows what he’s talking about and Carrier is only an amateur. Barnes says Carrier doesn’t even understand what fine-tuning is. Carrier quotes a couple of genuine scientists, but they are a minority, and Carrier apparently thinks that quoting a small number is sufficient to stand against the broad consensus that Barnes references.
It is hard to understand why Carrier has returned to this part of the argument, because he’s clearly arguing against the evidence, something you would expect he, as a naturalist, would be opposed to.
The theistic argument based on fine-tuning
Carrier makes much of Barnes not responding to his arguments here, and quotes two papers that oppose the theistic argument. But Barnes has not really addressed the theistic argument and it is hard to see from this exchange what he thinks of it. His interest (in this discussion at least) is in the facts of science and mathematics.
It is disconcerting to observe that Carrier seems to confuse the scientific facts and the theistic argument that builds on the facts, and thus seems to think that what he sees as a strong anti-theistic argument somehow changes the scientific facts.
Understanding probability
In his final two posts (referenced above), Barnes attempts to show that Carrier is way out of his depth when dealing with probability. (I suggest, if you read his posts, you skip the maths unless you are a mathematician, and just read the text.)
Barnes argues that:
- Carrier shows much confusion about basic probability concepts.
- Carrier confuses and mixes frequentist and Bayesian probability, two approaches that have quite different bases.
- He doesn’t seem to be aware of the mathematical axioms and proofs behind the two different branches of probability theory.
- Carrier’s novel approach isn’t endorsed by any of about thirty mathematicians that Barnes has read on the subject. Until Carrier publishes it in a peer-reviewed journal, any novel approach cannot be taken seriously.
Of course, I am not a mathematician, or a scientist, so how can I know whether Carrier or Barnes is correct on all this? Several reasons lead me to believe Barnes is basically correct:
- Barnes, as a cosmologist, uses probability in his professional life, whereas Carrier, as a historian, does not – although he has written on probability and history, his views haven’t generally been accepted (see below).
- Carrier is trying to support what appears to be a dogmatic view of the historicity of Jesus, based on probability, so seems more likely to have external reasons to argue the way he does, whereas Barnes appears to have no such agenda.
- I haven’t attempted to follow the mathematics in detail, but Barnes’ general arguments make more sense to me.
- Others have also concluded that Carrier has a poor understanding of probability – e.g.
- Jim, an atheist and a mathematical scientist has written quite critically of Carrier’s understanding of probability – e.g. “a misunderstanding of what the differences between Bayesian and Frequentist statistics” and “I felt there were severe errors with his arguments”,
- Jeffery Lowder’s criticisms of Carrier’s side of his argument with Barnes included significant criticisms of his ideas on probability. Lowder hasn’t yet commented on the latest exchanges.
- Tim McGrew, a philosopher specialising in probability and a christian makes a number of significant criticisms (in the comments on this blog), and
- “Tim Hendrix” (an anonymous commentator whose religious views I don’t know, but he doesn’t think the fine-tuning argument for God is very convincing, and he appears to know probability very well – could he be Tim McGrew?) takes apart Carrier’s statements on probability in detail.
What does all this prove?
It is an often-quoted aphorism: “There are lies, damned lies, and statistics.” Presumably probability estimates can fit in there somewhere close to statistics.
This brief review shows that probability is a difficult subject (did you need to be told that?). It is easily done badly, and easily misused, often due to faulty assumptions. No doubt I’m as likely to get it wrong as any other amateur.
I think we must be careful who we believe on probability, and prefer those who have real knowledge and experience in its application. I will always be wary of someone who is not well qualified and who argues that all the experts are wrong.
Picture: Bayes Theorem in lights, by mattbuck, in Wikipedia. You might wonder why anyone would make a neon sign of Bayes Theorem. It is, or was, at the offices of HP Autonomy, a computer software company, at Cambridge, UK.
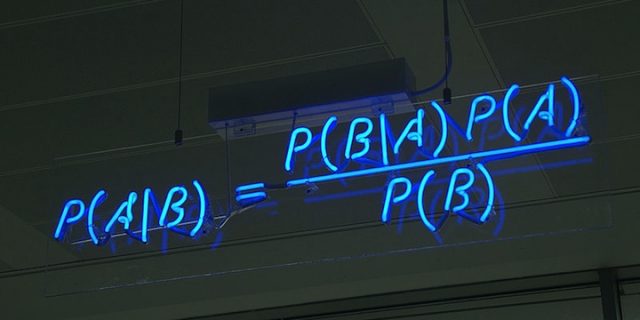
I do not understand probability theory at all, but I do understand one thing. Fine tuning argument is not at all necessary for proving the existence of God, because it can also be proved even if there is no fine tuning. Here is a link below:
https://sekharpal.wordpress.com/2016/01/11/is-fine-tuning-actually-required-for-proving-the-existence-of-god/
Again, if God is simple, as claimed by some of the theists, so the evidence of his existence that he has kept for us is also supposed to be as simple as God. So I simply cannot understand as to why so much lengthy and complicated arguments will be actually necessary for proving the existence of God.
I don’t think the arguments need be all that lengthy or complicated, but some people find arguments like this helpful or challenging, and like to analyse them, and others do not. We are all different! I happen to be one of those who find them helpful.
What convinces you?
If complicated arguments are essential for proving the existence of God, then that shows that God as a subject is also complicated, not simple. In that case one should not claim that God is simple, because this claim is not justified.
Thanks for the shout out, Eric!
“Simple” is a technical term in theology, Himangsu. It means that God is not composed of parts. It does not meanthat God is easy to understand, or that the arguments for his existence have to be short and obvious.
Hi Aron, thanks for your blog, and your comment.
Hi Himangsu. I agree with what Aron says about the simplicity of God, but it’s not a concept I think is very important or meaningful, so I don’t think I ever talk about it. Is it important to you? Why do you believe?
Mystics have repeatedly said about their God that he is spaceless and timeless. If God is spaceless and timeless and if this God is really there, then there is an everlasting state of spacelessness and timelessness in this universe, because this God is everlastingly present with all his attributes. So, if there is a God, then in that case there will be this universe plus the presence of this everlasting state of spacelessness and timelessness. Whereas if there is no God, then in that case there will be only this universe and nothing else. If there is the presence of an everlasting state of spacelessness and timelessness in addition to this universe, then space and time in our universe cannot be absolute. For space and time to be absolute, they will have to have the same values in each and every case without any single exception. But due to the presence of this everlasting state of spacelessness and timelessness, space and time will have null values in at least one case, that is, in case of God, whereas in every other case they will have non-zero values. Thus it can be seen that due to the presence of this everlasting state of spacelessness and timelessness in addition to the universe, space and time in our universe will become relative. Special theory of relativity has also shown that space and time are indeed relative. So, if special theory of relativity is not a pseudo-science, then mystical experience is not a hallucination. That means if special theory of relativity is not a pseudo-science, then this spaceless and timeless God is real, and not merely an apparition as claimed by the atheists.
Therefore either special theory of relativity is not a pseudo-science, in which case we will have to admit that there is a God. Or it is merely a pseudo-science, which will mean that there is no God.
One more point. If anyone on this earth can show that despite the presence of an everlasting state of spacelessness and timelessness in this universe space and time can still have absolute values, then let him/her show it. In that case we will also have to admit that there is no God.
When a Christian starts using complex mathematical formulas and philosophical theories to defend his belief in first century corpse reanimation-transformation (aka:
resurrections)…I yawn.
I yawn because it is soooo silly.
I know for a fact that if a Muslim attempted to use these same ploys to defend the veracity of Islam’s claim that Mohammad flew to heaven on a winged horse, the very same Christians would snicker and hand-wave away these arguments without giving them a second thought, believing that these tactics are nothing more than an obvious, desperate attempt to dress up a superstition as believable reality.
This is really thought-provoking. I don’t know about others but I believe God’s existence and I don’t need complicated arguments or formulas to prove that because that’s my belief.
Hi Aika, I’m glad to have provoked thought! I’m also glad you believe. Some people find scientific evidence helpful, others not so much, but I think it is OK to be either.
Quite a very insightful article and indeed we may tend to either over-simplify or over-complicate things. I was just thinking about around a thousand years ago devoid of all the academicians, scientists and skeptics how simple was the belief system of our ancestors, in all probability.
Yes, I think life in general was simpler back then. But we have made progress in many things, gone backwards in others, and it can never be the same. All belief systems must now account for amny more known facts. Thanks for your comment.