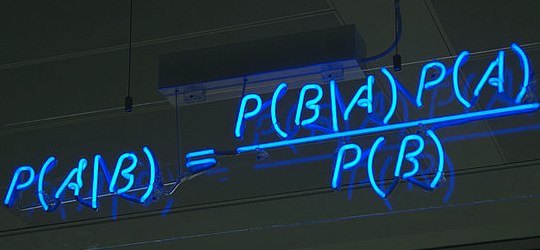
I am a bit of a maths nerd – I enjoy using spreadsheets and graphs to analyse and illustrate. But I can’t claim much expertise – I did once obtain a Distinction in Statistics at Uni, but I’ve forgotten all of that now.
So while writing up some material on healing miracles (see Healing miracles around the world and Healing miracles and God) it occurred to me that miracles were a subject just asking to be looked at statistically. But it certainly wasn’t easy.
If you’re not a maths nerd, I suggest you read the summary only, which I’ve thoughtfully placed at the top.
Let’s start with the conclusion
After I did a bit of reading, a lot of work on a spreadsheet, and an amount of head-scratching and re-calculation, I came to the conclusion that accounts of apparent miracles which occurred after christians prayed for healing provide good evidence for the existence of God. But the maths required a number of assumptions that really need to be better based before I would hang my hat on the results.
Non maths nerds can quietly leave now if they wish. For the rest, here’s how I came to this conclusion.
Bayes Theorem
Bayes Theorem is an established calculation of probability that assesses how new information changes the probability of some fact. If we apply it to miracles, the calculation requires the estimation of the probability of a particular miracle occurring if we assume God does exist, and the probability of it occurring if we assume God doesn’t exist.
The analysis of miracles
The question I wanted to consider was this. Do the many miracle accounts increase the probability that God exists? To consider this question, we need to consider probabilities for the following four cases:
| Person is prayed for | Person is not prayed for | |
|---|---|---|
| Person is healed | ||
| Person is not healed |
Estimating numbers
I don’t take these numbers all that seriously, but they are useful in giving an indication of my thinking and the evidence. So my estimates are as follows:
- The probability of someone recovering assuming there is no God, that is, by natural means, is occasionally reported. It is different for different conditions and diseases, but an estimate of 1 in 10,000 is reasonable. (It turns out this number isn’t critical, for the important thing is the ratio of this and the next figure.)
- The probability of someone recovering assuming God exists must include both this natural probability and the estimated probability that God might have intervened. I have assumed that if God exists, he might be as likely to heal someone as occurs naturally, so the total probability is 2 in 10,000. This isn’t a blind guess.
It is estimated from survey data that 300-400 million christians claim to have experienced or observed a healing miracle. If we make an estimate of how many people have seen more than one miracle, and how many miracles have been observed by more than one person, we may estimate the number of different miracles to be a smaller number, say 100 million. If we then eliminate 90% as not having occurred (a pretty severe estimate) we are left with 10 million unexplained healings experienced by 2 billion christians, a probability of 1 in 200, much more than the estimate I have actually used.
- We also need a starting probability of God existing, and to avoid any christian bias, I have used 1 in a million.
This then gives the probabilities shown in this table:
| Person is prayed for | Person is not prayed for | |
|---|---|---|
| Person is healed | 0.0002 | 0.0001 |
| Person is not healed | 0.9998 | 0.9999 |
Doing the calculation
We are interested in the results for people who pray for healing, on the assumption that these give an indication of the existence or otherwise of God. For every ten thousand people who pray for healing from a serious condition, we are assuming two are healed and 9998 are not. (Again I say that I believe the success of prayer is much greater than this, but I am trying to use the most unfavourable numbers.)
So we do a step-by-step Bayesian calculation, where the initial probability of God’s existence is reduced by a very small amount for each non-healing and increased by a larger amount for each healing.
And the answer is ….
It turns out that it after we have considered 35,000 people, or 72 apparent healings, the probability that God exists has risen from 1 in a million to 50%. When we have considered 43,000 people and 83 healings, the odds have risen to 90%.
So what does this show?
If we believe the numbers, it shows that it only takes a relatively small number of well-attested healings to make it highly likely that God exists. And that number of well-attested healings certainly exist. Even just using the ones I have documented as Healing miracles and God we reach that number.
Of course the numbers are very rough estimates, and undoubtedly could be contested. But I have been fairly conservative, and I have played around with other numbers, and while the numbers can change a lot, the conclusion doesn’t change much.
I have to admit that the whole approach is problematic – is it really valid to try to estimate the probability of God’s existence? But besides being a fun exercise, the calculation helps make clear the assumptions each of us make.
I’d love feedback
Perhaps there are errors in my assumptions, method or computation – if so I’d like to have them pointed out so I can improve it. Any other feedback is welcome.
Read more
- Healing miracles and God – a summary of my investigations so far.
- Can we scientifically test alleged healing miracles? – some thoughts on how we should go about this.
- Ten healing miracles – how a doctor investigated the medical facts.
- Healings at Lourdes – background information on one of the world’s most famous places of healing.
- More healing miracles – reports from around the world.
- Heart-starting action – a miracle in the emergency ward.
Photo: Wikipedia
I think you have a fundamental flaw here. How can you claim, even theoretically, to be able to separate people prayed for and not prayed for? In this “Christian nation” of ours, how many sick people are not prayed for? And how would you know? You simply have no control group. You could theoretically run a scientific experiment along these lines, but one hasn’t already been done for you out in the world.
Granted, even one proven healing miracle could prove the existence of a higher power. But I fail to see how your numbers game adds to that claim.
Hi Kevin, thanks for reading and making a comment. For Bayes Theorem, we don’t need to know which people or what percentage are prayed for, or not. Those aren’t terms in the equation.
What we have to estimate are the probabilities that someone is healed if they are prayed for and if they are not. (The probabilities that they are not healed of course follow from that.)
Of course I don’t know these probabilities, I have just made estimates. But they show that we don’t need all that many plausible miraculous cures to make the probability of God very high. Change my estimates in any reasonable way and the conclusion isn’t that much altered. Why not try some examples yourself. It is easy if you use a spreadsheet. And then tell us what you find?
Isn’t that wonderful UnkleE?!?!
“But they show that we don’t need all that many plausible miraculous cures to make the probability of God very high. Change my estimates in any reasonable way and the conclusion isn’t that much altered. ”
So in other words, it doesn’t matter which data we use, “the conclusion isn’t that much altered”. The same conclusion will be reached, no matter how we go about getting there. The probability of god is “very high”
And you are going to sit here with a straight face and tell anyone that you haven’t already pre-decided the outcome and that nothing that anyone can say or any data they use in this particular argument is going to change your mind that “the probability of God is very high”? And then pretend that you are willing to have an open and honest discussion on the matter? Who, exactly, are you trying to kid?
Hi Ashley, thanks for reading this. I gather you don’t like the conclusion, but it is based on the information I had. Where would you disagree with my approach or my numbers?
Where would I disagree with your approach and your numbers?
You’re joking right?
You use an approach to solving a problem and claim afterwards that it doesn’t matter which data you use, the result won’t be altered in any significant way – and you’re asking me if I disagree with this approach? Can you possibly be serious? The conclusion has already been pre-decided and the data is nothing more than aesthetic window dressing which has little to no bearing on the outcome. You can’t get any more anti-scientific and anti-math than that.
Hi Ashley, no I’m not joking. I am a dad, and I do tell “Dad jokes”, but you can usually tell they are meant to be funny even if they’re not. 🙂
I am not just using some random approach to solving a problem, but Bayes Theorem, a well-established formula in probability. I outline the reasons for my choice of the values I enter into the formula. If you (or anyone else) think I’m wrong, I would be keen to see alternative estimates with justification, or a corrected calculation if you think I’ve done the numbers wrongly.
I know you hate me saying I’m right and you’re wrong, but we’ll both just have to grit our teeth and cope with it, because I think your next couple of statements are misunderstandings.
“it doesn’t matter which data you use, the result won’t be altered in any significant way”
Whenever we make estimates of values, it is usual to do some sort of sensitivity analysis, to see if the final result changes much if we change the estimates a bit, to reflect the uncertainty in them. That is what I did, and this showed that variation in the estimates changed the final number a bit, but not in a way that changed the conclusion much. Of course if you’d changed the estimates by a large and unreasonable amount, you’d get a very different result. But the evidence doesn’t (in my opinion) allow that. But I have invited you to consider the evidence and suggest different estimates. I will happily put those into the equation and tell you the results.
“The conclusion has already been pre-decided and the data is nothing more than aesthetic window dressing which has little to no bearing on the outcome.”
This is technically a logical fallacy, perhaps the one known as “ad hominem” or perhaps “poisoning the well”. Instead of offering evidence and reason to critique someone’s argument, personal attacks are offered instead. It isn’t a very courteous way to respond, it doesn’t address the evidence and the argument, and perhaps most important of all, it makes a claim that you can’t possibly know or justify.
It so happens that you are mistaken. I had no idea how the calculation would turn out mathematically, except I thought it logically should show something. It did. Again, I invite you to address the evidence, the estimates and the calculation. I am quite open to the idea that my statistics isn’t world-beating, and therefore to correction.
Of course if you can’t critique the evidence, estimates an calculation, maybe as a thoughtful person you might consider the conclusion a little more seriously?
Thanks.
I am utterly shocked UnkleE! I’m obviously the one who doesn’t understand and I am the one who is mistaken! I must say I didn’t see that one coming!!!!!
“But I have invited you to consider the evidence and suggest different estimates. I will happily put those into the equation and tell you the results.”
What difference does it make what estimates I use for the values that you put into the equation?!?!?! You have already openly stated that as long as my estimates remain “reasonable” (reasonable according to YOU I assume) it will have little to no bearing on the outcome!!!!!! Your own words: “Change my estimates in any reasonable way and the conclusion isn’t that much altered.” Why would I bother getting you to plug numbers into an equation in which the outcome will be virtually the same no matter what? What possible point could there be in that?!?!?!?!?!!?
“This is technically a logical fallacy, perhaps the one known as “ad hominem” or perhaps “poisoning the well”. ”
No sir, this is not “technically a logical fallacy known as “ad hominem” AT ALL An ad hominem is the type of argument that attacks the person and not the argument. For example, If I had said UnkleE is from Australia and we know that people from Australia are terrible at math, therefore we cannot trust his experiment or its conclusion – THAT would be an ad hominem. I have attacked your approach to the problem. The outcome is pre-decided, It doesn’t matter what numbers you use in the equation. I have not attacked you personally. You are being dishonest and disingenuine.
In any event, the comment still stands, You have decided to use Bayes theorem. It is a well established formula in probability. That’s nice. That has absolutely no bearing whatsoever on whether or not it is the correct formula to use for this particular problem. The fact that it gives you virtually the same result, no matter what numbers and data you use, should give you pause to consider whether or not you have chosen to use the correct formula. You have constructed the equation such that the data will not change the outcome – that the probability of god existing is very high. It is not the conclusion that I don’t take seriously, it is your approach to solving the problem. You seem to think that my problem is with the numbers you used in your equation. It is not. It is the equation itself. Your equation will confirm the extremely high probability of god existence, no matter what numbers you plug into it. I am suggesting that perhaps your equation just may be biased to provide you with a conclusion that you want to see. Maybe as a thoughtful person you might consider your approach to the problem a little more seriously?
But no need to answer me UnkleE. I already know that yo have chosen the correct formula, that the approach is the correct one, and that the results shouldn’t Be questioned. Clearly, it must be me who is misunderstand (still) and mistaken (still). As usual UnkleE, you’re right, You’re always right.
Hi Ashley, in discussions like this, I have always been under the impression that when I want to criticise a viewpoint, I need to offer both evidence and reasoned argument. If I offered scorn, or mere assertions, it would mean nothing.
Now you have commented on this post and you are not happy with my conclusions. I have asked a couple of times if you have alternative evidence to offer, or how you would correct my calculations. So far you have done neither. I think scorn and mere assertions accurately describes your response. So it means little.
So I invite you again to offer a reasoned response to the evidence I refer to and/or the calculation I performed.
Just to clarify one misunderstanding. I didn’t require you to use estimates I think are reasonable, as you infer. I said my calculation was based on estimates I thought were reasonable (you wouldn’t expect me to use ones I thought unreasonable?), but I invited you to “consider the evidence and suggest different estimates.” All I asked is that you provide “justification” for your estimates, similar to what I have done.
So, the ball’s in your court. I understand you don’t like my conclusions and want to find a way to discredit them, but can you offer evidence and reasoned argument rather than scorn and assertions?
“Now you have commented on this post and you are not happy with my conclusions. I have asked a couple of times if you have alternative evidence to offer, or how you would correct my calculations.”
You clearly did not read my last post because if you had, you would not be saying that. For what has to be at least the 3rd time now, it is not that I am “not happy with your conclusion”. I have repeatedly critiqued your METHOD for getting to your conclusion. A METHOD that always gets you to the same conclusion, no matter what data you use to get there, is clearly flawed. I hope it will be the last time I have to say that in order for you to accept that. Has it sunk in yet UnkleE? METHOD. Not conclusion, METHOD.
Repeat after me. “Ashley wants me to re-examine my METHOD”. “The METHOD”. “The METHOD” “Ashley wants me to re-examine my METHOD”.
“Hi Ashley, in discussions like this, I have always been under the impression that when I want to criticise a viewpoint, I need to offer both evidence and reasoned argument.”
I know you are under that impression UnkleE. That is because you clearly cannot grasp the concept of the Burden of Proof. I do not have any alternative evidence to offer because I am not trying to prove that god does not exist, nor am I trying to prove that miraculous healing does not occur. I readily admit that I have no evidence to offer that would prove that god does not exist and that miraculous healing does not occur. I readily admit that I do not have any evidence that proves for certain that you are wrong. The only thing I have to offer is the critique of your method. I think it is severely flawed. You have already openly stated that you will arrive at more or less the same conclusion regardless of the data that you use. If you cannot see the flaw in your method, then you cannot see the flaw in your method.
If you ask me how I could correct your calculation, I would suggest that you go back to the beginning and start over. Not to the calculation part, but the formation of the hypothesis and formula (equation) used. In other words, develop a new METHOD. A formula (equation) that may actually yield a different result when you use different data would be a gigantic leap in the right direction.
Hi Ashley, I am quite aware you don’t like my method, which consists simply of applying Bayes Theorem to the evidence using some estimates. My question was what exactly is wrong with it and how would you improve it?
But since you don’t seem to want to and don’t seem to want to make any statements any more (for if you did then they would have a burden of proof) then I really don’t need to say any more. Thanks for taking an interest.
One minor correction. You say “You have already openly stated that you will arrive at more or less the same conclusion regardless of the data that you use.” But I did not say that. I said the numerical answer would be different but the conclusion would be much the same for any numbers that I thought were reasonable. I invited you to offer numbers you thought reasonable.
“My question was what exactly is wrong with it and how would you improve it?”
Which I have answered, THREE TIMES ALREADY. TRY ANOTHER EQUATION. One that doesn’t lead to the same answer no matter what data you use. May I suggest trying different equations which at least have the possibility of yielding an answer that you won’t agree with perhaps? If you had another equation that would yield a high probability of god existing , but could also yield a low probability of god existing, depending on the data you used in the equation, your result might be a little more credible.
But don’t worry about it UnkleE. I pointed that out 3 times already and it’s already gone in one ear and out the other so I don’t expect that by repeating it a 4th time, it will make any difference. Clearly, you are right and I am wrong. And by strange co-incidence, I seem to have once again stumbled on the pattern that you exhibit when you converse with people with whom you disagree… Disagree, mistaken, misunderstand, stop.
You are the most amazing individual this planet has ever known.
Ashley, can you suggest another equation? I don’t know another one.
Hi unkleE
Ok so this is an old post so I completely understand if you don’t see this comment. But I was wondering if you could show me how you did this calculation, as I am just not getting the same results you are.
Bayesian analysis usually uses an equation that looks like this:
P(A|B) = P(A) X P(B|A) /
P(B)
In the above example P(A) would represent the probability that God exists on its own, which you put at 1 in a million.
P(B) is the probability that someone would be healed without any involvement from God, which you put at .0001
P(B|A) is the probability that someone would be healed given that God exists, which you put at .0002
Now what we want to know is P(A|B), which is the probability that God exists, given someone is healed. So we plug in the numbers
.0000001 [P(A)] X .0002 [P(B|A)] / .0001 [P(B)] = .0000002 [P(A|B)]
Or in other words, using the values you gave above the probability that God exists given someone is healed, is 2 in a million. I simply don’t see how you are getting the 50% and 90% figures.
As such can you please lay out, as I have done above, the equations you are using and how you are plugging in the numbers. I suspect it is simply a case of it not being clear what numbers you are using, so if you can clarify this I would appreciate it. Thanks
Hi RabbitPirate, thanks for reading and taking an interest. It is getting late, so I’ll have a go at what I think is the answer, and if it isn’t, let me know and I’ll spend a little more time on it.
As I understand it, Bayes Theorem is a formula for updating a probability estimate when new information is obtained. Every time we get new information, we can update our estimate.
So we have millions of people suffering illnesses, some are prayed for, and some are not, some recover and some do not. Each situation is a new piece of information, and therefore we can apply Bayes Theorem to each situation.
The key, I think, that you haven’t taken account of, is this sentence: “So we do a step-by-step Bayesian calculation, where the initial probability of God’s existence is reduced by a very small amount for each non-healing and increased by a larger amount for each healing.”
Thus I found that: “after we have considered 35,000 people, or 72 apparent healings, the probability that God exists has risen from 1 in a million to 50%. When we have considered 43,000 people and 83 healings, the odds have risen to 90%.” (I used a spreadsheet to do that repetitive calculation.)
So your calculation is correct, I think, but you have only considered the first piece of information. But obviously each new piece of information adds to our knowledge, and the more examples we have of unexplained recoveries, the more probable divine healing becomes.
I am not a statistician, but I think that computation and the logic behind it are correct. If you have any corrections, I would be very pleased to hear them.
Thanks again.
Hi unkleE
Thanks for you quick response, I do think I understand where you are coming from better now. Please correct me if I am wrong, but what you seem to be saying is that you are setting an initial value for the probability of God’s existence at 1 in a million [P(A)] and you are running this through the equation with the healing information to get a revised probability of God’s existence of 2 in a million [P(A|B)].
Then, and I think this is where the mistake is occurring, you are feeding that 2 in a million number back into the equation as the new P(A). You are then repeating the process over and over again until, after 35,000 patients and 72 healings, you arrive at a probability for God’s existence of 50%? Is that correct?
If it is, and I will admit to being no expert on Bayesian Analysis, then I believe you are making a fundamental error. Using the method you have outlined then you would always end up with a large probability, regardless of the topic at hand.
Try this, re-run your equation with the exact same values, but change “Person is prayed for” to “Person receives psychic healing”, and “Probability that God exists” to “Probability that Psychic powers exist”. If you use the exact same values as before and do the exact same equation you did before then, after running it through the loop 35 times, you will end up with a probability that psychic powers exist of 50%. Do you think this is really the case?
Indeed we could run this same experiment countless times, each time changing the thing we wish to investigate, and every time we would come up with a 50% probability value after looking at 35,000 patients. Clearly this indicates that there is a problem with the way that you are running things.
My understanding of Bayesian Analysis is that you have a hypothesis you wish to test (God’s existence) and you want to see if the probability of your hypothesis increases in the face of evidence (healings). You started with a prior probability of God’s existence of 1 in a million, you then looked to see what the 1 in a thousand additional healing you would expect to see if God exists would do to the probability of his existence. And you got your answer, it increases it to 2 in a million. But that is where you should have stopped.
You do not then feed the posterior probability back into the same equation as the new prior probability, that is just not how it works. The posterior probability IS the answer to the question you asked.
“If we assume a prior probability of God’s existence of 1 in a million, how is that probability affected if we look at the evidence for miraculous healings?”
Your answer is that the probability for God’s existence increases to 2 in a million. That is the final answer. Sorry, but I think you got the answer you did because you used Bayesian Analysis incorrectly.
Hello again,
I think you have raised two main points, one of which I have questions over too, and one of which I think it a misunderstanding. First the misunderstanding (as I see it).
You say: “You do not then feed the posterior probability back into the same equation as the new prior probability, that is just not how it works. The posterior probability IS the answer to the question you asked.” But that is exactly what we do with Bayes.” Let me give a neutral example.
Suppose we are testing a new drug and want to know the probability that it cures cancer. If we have 100 people on a trial program and 3 of them die, 10 of them fully recover and the remainder are still receiving treatment. If we followed your proposal, we would just apply Bayes to one of the results (but which one, since there are negative and positive?), which obviously wouldn’t be right.
Now perhaps, if we were smart enough, we could calculate the odds of 10 recoveries and 3 deaths in one calculation, but I don’t know how to do that. And anyway, when we get some more results, we’d have to do a new calculation anyway. But with Bayes, we can do a simple calculation, then another, one for each result, and it doesn’t matter what order we do them in.
So that is the method, and I’m pretty sure that is broadly correct. If we did it your way for the healings or recoveries, then we’d only be considering the evidence for one healing. But if there were 1000 recoveries, that would be more remarkable, and if there were 1,000,000, that would be even more remarkable. So we have to consider them all.
“Try this, re-run your equation with the exact same values, but change “Person is prayed for” to “Person receives psychic healing”, and “Probability that God exists” to “Probability that Psychic powers exist”. If you use the exact same values as before and do the exact same equation you did before then, after running it through the loop 35 times, you will end up with a probability that psychic powers exist of 50%. Do you think this is really the case?”
This is an interesting question that I too have pondered. And I think it really would be the case if and only if the probabilities were the same. So, let’s examine that.
1. Is the initial probability that psychic powers exist 1 in a million? I would accept that as a reasonable start.
2. Is it true that the if psychic powers don’t exist, the probability a person will recover anyway (i.e. spontaneous remission) is 0.0001? Yes, this is the same as in my example, no change.
3. Is it true that if psychic powers do exist, then the probability of a person recovering is 0.0002 – that is 0.0001 that they will recover naturally and 0.0001 that psychic healing will work for them? I’m less sure of this one. I provided a basis for my estimate of healing, but I don’t know if there is the same basis for psychic healing.
4. How many people seek psychic healing and how many claim they have received it? Here I very much doubt we would have 300 million psychic healing claims, though I have no idea how many there would be.
So I don’t think the two situations can be compared, unless we have data that shows something more than I know now.
“Indeed we could run this same experiment countless times, each time changing the thing we wish to investigate, and every time we would come up with a 50% probability value after looking at 35,000 patients. Clearly this indicates that there is a problem with the way that you are running things.”
This the question I have asked myself too. How does Bayes deal with multiple possible causes? For example, what if people sought christian prayer AND psychic healing AND medical healing, how do we separate out the possible causes and compute the probability? I don’t know.
I don’t have the problem that you have, because I believe if the numbers are correct, the calculation is correct. My problem is with designing the experiment and interpreting it. Bayes Theorem only deals with one hypothesis (e.g. “God exists” or “Psychic healing works”) and it’s negation (“God doesn’t exist” or “Psychic healing doesn’t work”).
My thought is that we only address one question at a time, but we have to include all other factors into the analysis.
So, when I say the probability of healing if God doesn’t exist is 0.0001, then I am including spontaneous remission and psychic healing in that number. And perhaps that means the estimate needs to be changed. But even if I do that, I may still show that both hypotheses are reinforced by the experiment, which is troubling. Although of course it may be that both forms of healing “work” sometimes.
I don’t know, I’ll have to think about it some more, and probably try to find a forum where I can ask a few questions.
What do you think about what I have said here? Do you have any strong beliefs about God healing or psychic healing?
Thanks for your interest, I really appreciate the opportunity.
Eric
Hi unkleE
So for some reason your last reply only came through to my email and doesn’t seem to have appeared on here. As such I will make sure I include quotes from you so it is clear what I am responding to.
“Suppose we are testing a new drug and want to know the probability that it cures cancer. If we have 100 people on a trial program and 3 of them die, 10 of them fully recover and the remainder are still receiving treatment. If we followed your proposal, we would just apply Bayes to one of the results (but which one, since there are negative and positive?), which obviously wouldn’t be right.
Now perhaps, if we were smart enough, we could calculate the odds of 10 recoveries and 3 deaths in one calculation, but I don’t know how to do that. And anyway, when we get some more results, we’d have to do a new calculation anyway. But with Bayes, we can do a simple calculation, then another, one for each result, and it doesn’t matter what order we do them in.”
Well first up I would not use Bayes for that sort of test. In that example we are not looking to see if the probability of something increases in the face of additional evidence, but whether the drug we are testing produces a statistically significant increase in the number of patients who recover. It is an entirely different situation from the one outlined in the post above. In that case I would use something like an F test or maybe an ANOVA.
“So that is the method, and I’m pretty sure that is broadly correct. If we did it your way for the healings or recoveries, then we’d only be considering the evidence for one healing. But if there were 1000 recoveries, that would be more remarkable, and if there were 1,000,000, that would be even more remarkable. So we have to consider them all.”
Ok I think I am seeing where the confusion lies now. In the post above you talked about the number of people healed who aren’t prayed for (0.0001) and the number of people healed who are prayed for (0.002). These number represent recovery rates, not the number of people healed.
As such it doesn’t matter if we are looking at a thousand people or 300 million people, the recovery rate is still 0.0001 for those not prayed for, and 0.0002 for those who are prayed for. It is the recovery rate that matters, not the specific number of recoveries. You don’t need to re-run the analysis for every additional thousand people, you have the rates of recovery that apply regardless of how many people are involved.
What this means is, if we run the equation for a thousand patients where we would expect to see 1 recovery without God and 2 recoveries with God, the numbers we put in look like this:
P(A|B) = .0000001 [P(A)] X .0002 [P(B|A)] /
.0001 [P(B)]
And if we run the equation for 35,000 people, where we would expect to see 35 recoveries without God and 72 recoveries with God, the numbers we put in look like this:
P(A|B) = .0000001 [P(A)] X .0002 [P(B|A)] /
.0001 [P(B)]
The recovery rate is exactly the same regardless of how many patients we are looking. 2 people in every thousand recover with prayer, and 1 person in every thousand recovers without prayer. You only need to run the equation once regardless of how many people are involved and you don’t feed the posterior probability back into the same equation as the new prior probability.
“This is an interesting question that I too have pondered. And I think it really would be the case if and only if the probabilities were the same. ”
It doesn’t matter if the probabilities are the same or not, it what you do with them that matters the most. Let’s say the prior probability of psychic powers is 1 in ten trillion. If we run it through the equation and get a posterior probability that is higher than this, say only 1.00000000000001 in ten trillion, and we then feed this posterior probability back in as the new prior probability and keep repeating this process over and over, we will always end up with an incredibly high posterior probability that psychic powers exist. We will get this because we are using Bayesian analysis incorrectly.
“This the question I have asked myself too. How does Bayes deal with multiple possible causes? For example, what if people sought christian prayer AND psychic healing AND medical healing, how do we separate out the possible causes and compute the probability? I don’t know.”
The simple answer is you don’t. It is the wrong tool for the job you are doing. You would probably want to use an ANOVA again in this case.
Hi, thanks again for your comments and your persistence.
1. First, my apologies for the comment coming by email. I have posted it here now so the discussion makes sense.
2. I really appreciate your comments, and if you are right, I will take the post down as being incorrect. But I still don’t think you are right. For instance, I don’t think ANOVA would be useful here at all – what are the two variances we are to compare? So it would be helpful to know what is the level of your statistical knowledge? Mine is little better than rudimentary.
3. To move forward, I have found a couple of Maths forums, and I intend to ask a few questions there to see if I can get some outside help. This will take a few days (at least), but I will comment back here in a few days. Please check back, as I think this discussion is very worthwhile.
Thanks again.
Hello again, sorry to take so long to get back to you. I tried to get advice from two maths forums, but no-one replied, so then I asked a couple of questions of this particle physics researcher who was writing on probability, and he seemed to agree that my approach was correct in principle.
So the only issue, I think, is with the numbers, and I make no claim about the numbers except that they are illustrative.
What this shows, I think, is that whenever any event is more likely if God exists than if he doesn’t (which must be the case with remarkable recoveries), then that is cumulative evidence for God existing. There are all sorts of events that may be used in this way, both for and against God’s existence, this is just one such set.
Hey unkleE
Hmm ok, well I must say I still feel slightly uncomfortable about the way that you are using Bayes here, but like I have said from the beginning, I am not an expert on this sort of thing so I could well be wrong. For example you are of course completely right than an ANOVA would be the wrong type of test for the data outlined above, I have no idea what I was thinking (I probably wasn’t to be honest) when I suggested that.
I am going to have to give this some more thought. I still think there is something fundamentally wrong with feeding the end result of the analysis back into a new set of analysis. It strikes me that even with the smallest of probabilities this method will always result in almost absolute certainty after you have run it a dozen or so times. This just seems wrong to me.
Anyway if you do hear back from those maths forums do let me know. If I am wrong about how Bayes works I would like to know it. I’ve enjoyed our chat, thanks. RP